What is the best form lens?

I recently came across an interesting question: “What is the best form of a singlet lens?” At first, it seemed trivial — the answer is clearly the plano-convex lens. That’s what many optical design texts suggest, since it minimizes spherical aberration and coma. But I soon discovered that this answer relies on certain assumptions.
The Simplest Model of a Best-Form Lens
The shape of a singlet lens is often characterized by the shape factor \(q\):
\[q = \frac{R_2+R_1}{R_2-R_1}\]where:
- \(R_1\) is the radius of the first surface of the lens.
- \(R_2\) is the radius of the second surface of the lens.
Many standard optical design textbooks identify the plano-convex lens as the “best form” when minimizing primary aberrations. The plot below, taken from Optical Systems Engineering by Keith Kasunic (and originally from Fundamentals of Optics by Jenkins and White), shows how aberrations vary with shape factor \(q\). Spherical aberration is minimized around \(q =0.714\), and coma is zero at \(q=0.800\). A plano-convex lens, with the curved side facing the collimated light, closely matches this ideal.
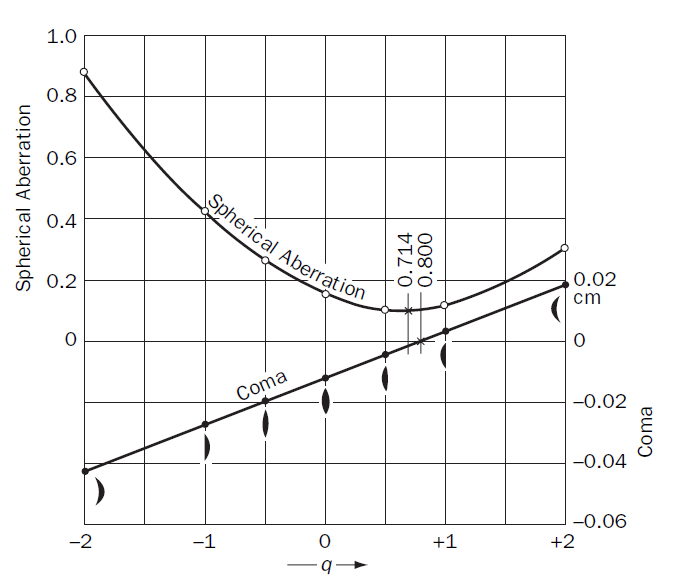
Figure from Optical Systems Engineering from Keith Kasunic
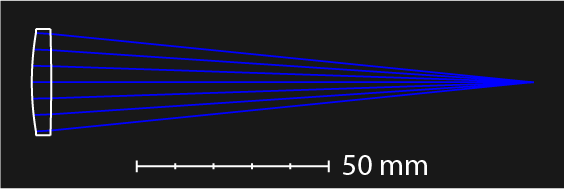
We can confirm this with a Zemax simulation. I designed a lens with the following constraints:
- Object at infinity
- Target focal length of 100 mm
- Entrance pupil diameter of 25.4 mm.
Below are the optimization results:
| Surface Type | Radius | Thickness | Material |
|---|---|---|---|
| (OBJECT) Standard | Infinity | Infinity | |
| (STOP) Standard | 76.889 | 5.000 | BK7 |
| Standard | -475.000 | 124.324 | |
| (IMAGE) | Infinity |
Not very surprising — it is a plano-convex — but things get more interesting when we consider the field of view.
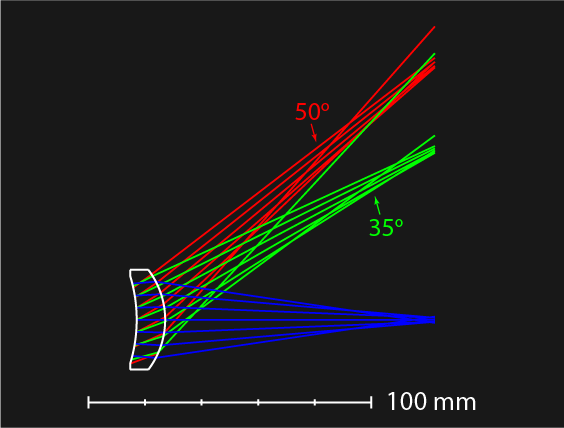
Adding Field of View Changes Everything
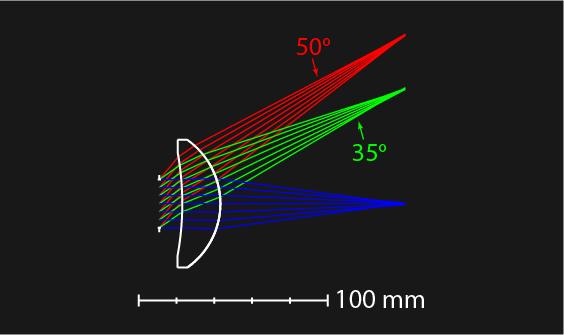
The plano-convex lens performs well for collimated light (on-axis). But what if we introduce a 50° field of view and optimize again? The result is no longer plano-convex. It’s a meniscus lens. Below are the optimization results:
| Surface Type | Radius | Thickness | Material |
|---|---|---|---|
| (OBJECT) Standard | Infinity | Infinity | |
| (STOP) Standard | -53.012 | 10.000 | BK7 |
| Standard | -28.987 | 94.699 | |
| (IMAGE) | Infinity |
Why Is a Meniscus Lens Better for Large Field of View?
This is quite fascinating—let’s delve deeper into the transverse aberration coefficients for spherical aberration (TSPH), coma (TTCO), and astigmatism (TAST).
Plano-Convex Transverse Aberration Coefficients:
| Surface | TSPH | TTCO | TAST |
|---|---|---|---|
| 1 | 0.0649 | 1.404 | 6.753 |
| 2 | 0.0610 | -1.722 | 10.80 |
| Total | 0.1259 | -0.318 | 17.55 |
Meniscus Transverse Aberration Coefficients:
| Surface | TSPH | TTCO | TAST |
|---|---|---|---|
| 1 | -0.229 | 3.185 | -9.841 |
| 2 | 3.3795 | -14.05 | 12.987 |
| Total | 3.1504 | -10.87 | 3.146 |
To interpret these values meaningfully, it is helpful to recall how each type of transverse aberration scales with pupil coordinate \(\rho\) and image height \(h\):
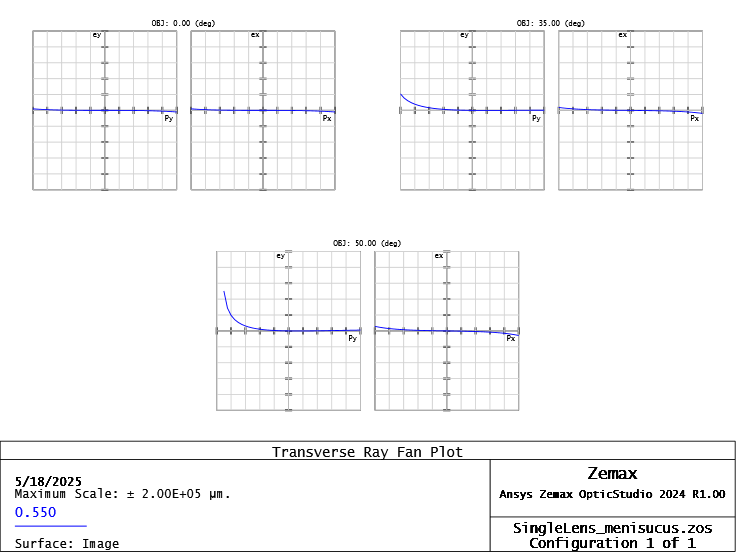
\[e_y(\rho, h) = TSPH\cdot \rho^3\]\[e_y(\rho, h) = TTCO\cdot \rho^2h\]\[e_y(\rho, h) = TAST\cdot \rho h^2\]Astigmatism in the plano-convex lens is high — and since it scales with \(h^2\), it quickly dominates at large field angles. The meniscus lens, though it has more coma, maintains low astigmatism, which is more important off-axis. This can be seen in the transverse ray plot below, where Plano-convex lens demonstrate large astigmatism at \(50^o\) field angle.The meniscus lens shows smaller overall error — except near the edge. This suggests we can do better by shifting the stop and optimizing again.
Plano-Convex Ray Fan:
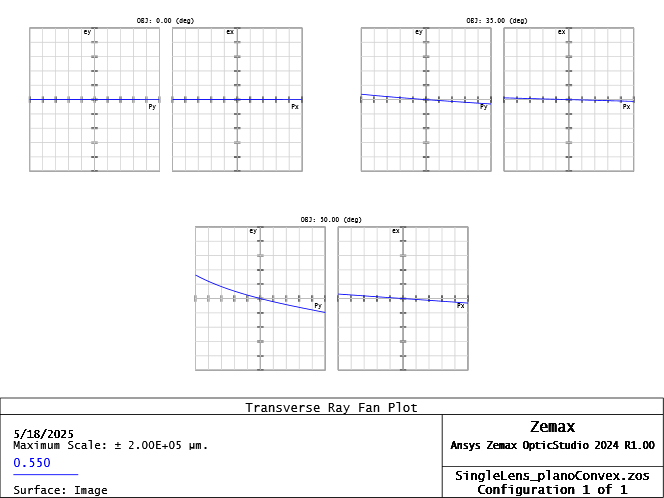
Meniscus Ray Fan:
Stop-shifted Meniscus Lens
If we stop-shift the meniscus lens, we can achieve a even better performance across all aberrations! The transverse aberration coefficients are further optimized.
| Surface Type | Radius | Thickness | Material |
|---|---|---|---|
| (OBJECT) Standard | Infinity | Infinity | |
| (STOP) Standard | Infinity | 12.052 | |
| Standard | -151.505 | 20.000 | BK7 |
| Standard | -41.130 | 97.046 | |
| (IMAGE) | Infinity |
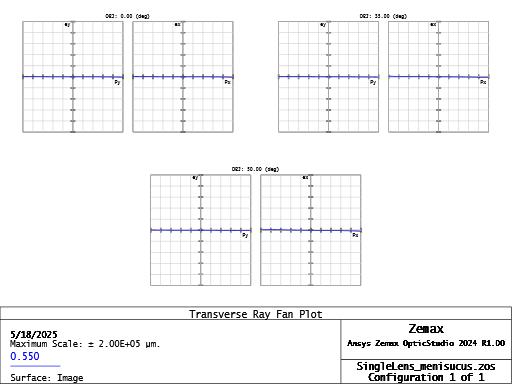
Stop-shifted Meniscus Transverse Aberration Coefficients:
| Surface | TSPH | TTCO | TAST |
|---|---|---|---|
| 1 | -0.006 | 0.267 | -2.326 |
| 2 | 1.525 | -1.098 | 0.176 |
| Total | 1.344 | -0.8318 | -2.150 |
Conclusion: Meniscus vs. Plano-Convex
Comparing the stop-shifted meniscus and plano-convex lenses:
- Plano-convex is excellent for on-axis and possibly small field-of-view application. It minimizes spherical aberration and coma — but suffers from high astigmatism.
- Meniscus, especially with a shifted stop, balances all three primary aberrations. It is ideal for wide field-of-view applications.
That is why simple eyeglass lenses, camera objectives, and AR/VR correction optics like those in the Apple Vision Pro often use a meniscus form. Even early cameras from 200 years ago relied on this basic principle.
What starts as a “trivial” answer reveals a much richer story — once we account for field of view.